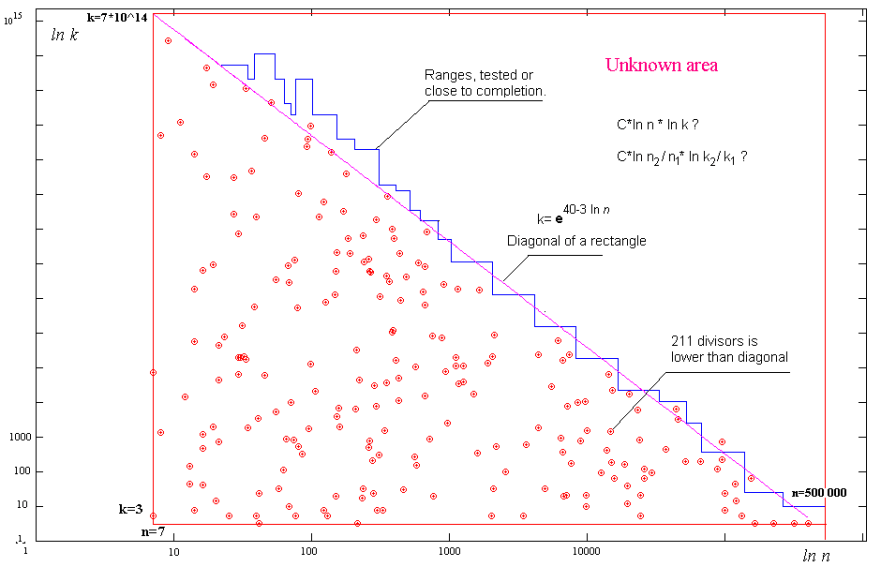
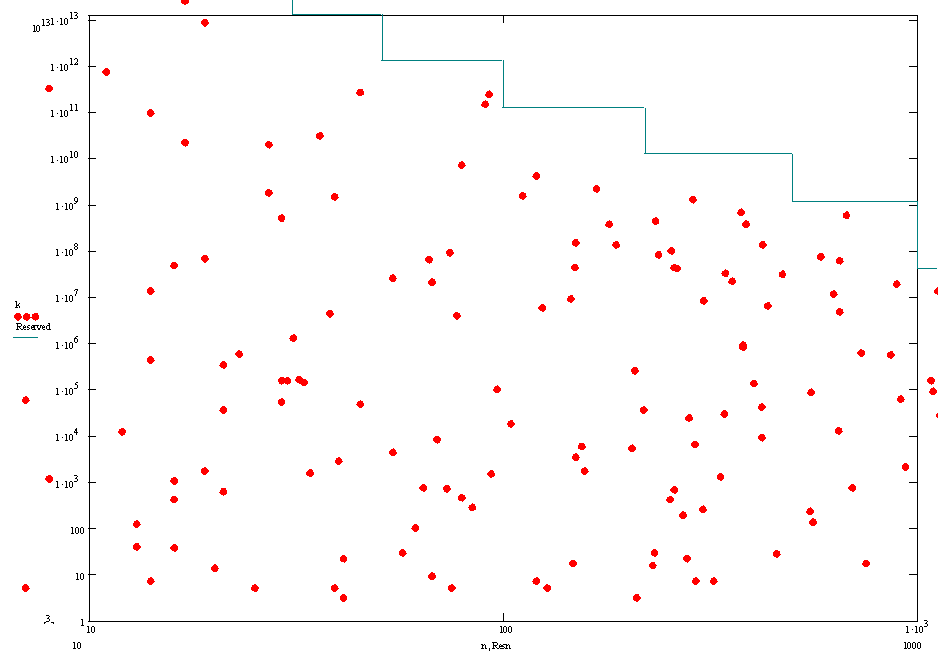
Here you can see all the Fermat number divisors on a logarithmic diagram. As you can see they are distributed almost uniformly. It appears that there are another 200 divisors waiting to be discovered inside the bounds of the above diagram.
Diagrams are available in MATHCAD format, click here.
This dependency can be expressed by the following formula. The number of Fermat divisors can be approximated by
where s is the correction factor. The behaviour of this dependency is a little complex.
| k | Known quantity | 0.8 ln(n).ln(k) | Divergence
|
|---|---|---|---|
| Status is completely known | |||
| 10^3 | 35 | 35 | 0 |
| 10^4 | 49 | 46 | +3 |
| 10^5 | 60 | 57 | +3 |
| 10^6 | 71 | 69 | +2 |
| 10^7 | 78 | 80 | -2 |
| 10^8 | 93 | 91 | +2 |
| 10^9 | 101 | 103 | -2 |
| 10^10 | 110 | 114 | -4 |
| Status is NOT completely known | |||
| 10^11 | 116 | 125 | -9 |
| 10^12 | 122 | 137 | -15 |
These results were collected on different hardware and software before, thus some mistakes may be present. There is a small probability that not all numbers have been found out for the calculated range. But the formula well describes known numbers. Increasing k 10 times for all n<500, it is possible to find approximately 10 divisors! If we have increased k 10 times for one number, then probability to find a divisor is 2%.
Guess. To find a Fermat divisor FOR ALMOST ALL n<500, we should increase k>10100.